|
Sam Kassegne, Ph.D, PE 1. Learning ObjectiveAfter completing this course, the student will: a) develope appreciation on the need to understand the basic assumptions used by a commercial structural analysis program. 2. IntroductionComputer-assisted structural engineering is now widely
adopted in the industry with most analysis and an increasing amount of
design tasks being automated. The availability of advanced analysis tools
based on finite element and matrix structural analysis concepts has enabled
engineers and architects to model, analyze and design innovative, complex
and unusual building and industrial structures.
The introduction and proliferation of such software analysis tools
has to be complemented by a firm and sound understanding of the fundamental
analytical concepts used in the formulation of the built-in analysis and
design algorithms. This course introduces engineers and architects to
these fundamental theories behind most structural engineering analysis
software commonly used in the profession. The course emphasizes on a discussion
of simplified but fundamental aspects of stiffness-based finite element
methodology that forms the basis for most structural engineering software.
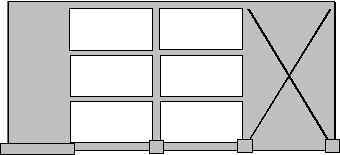
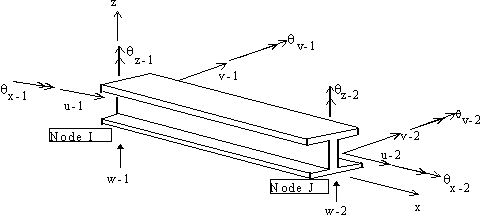
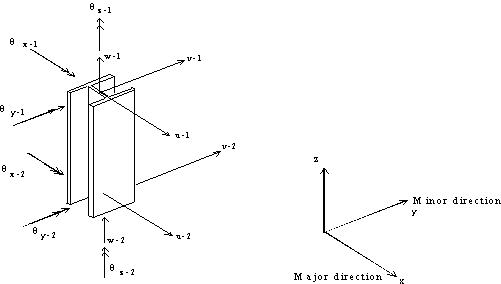
Important assumptions regarding the behavior of buildings are also included. For an elastic static and dynamic analysis, building and industrial structures can be modeled using a combination of beam, brace, column and wall elements. In some cases, two-dimensional elements like plate or shell elements are used to model the stiffness properties of a floor. Figure 1 shows a typical building frame modeled using beam, column, brace and shear wall elements. The stiffness coefficients of 3-Dimensional beam, column and brace elements are defined in terms of twelve degrees of freedom. These are the three rotations and three translations at each of the two nodes as shown in Figure 3 that correspond with axial, shear, bending and torsional deformations. Two-dimensional programs use reduced number of degrees of freedom because they ignore out-of-plane shear and bending actions. Results from such programs are acceptable only when out-of-plane actions and twisting of frames are nonexistent or negligible. It is also instructive to realize that some beam and column elements used in some commercial programs do not include the additional displacements due to shear deformations that could assume significant magnitude in deep beams and columns. Beam and column elements used in building and industrial structures also need to have the ability to model the effects of rigid end zones. Rigid end zones also known as panel zones do experience deformations that should be accounted for by the program. For brace and wall elements, these rigid end zones are typically ignored. Shear walls are typically modeled using a four-node isoparametric plane-stress finite element shown in Figure 3 [Reddy, 1987]. Since the basic four-node plane-stress element is a linear element, it tends to be too stiff in bending [Cook, 1981]. This will result in a non-conservative response [i.e., decreased drift] for buildings with tall wall panels where flexure is one of the dominant behaviors. To achieve a better performance under bending, incompatible deformation modes have been incorporated to this basic plane-stress element [Wilson, et al, 1974]. A wall element also needs to have in-plane rotational stiffness to accurately model moment continuity for beams and columns that frame into a wall system. This could be accomplished through several ways. One possibility is to use plane-stress elements that do have an additional in-plane rotational degree-of-freedom at each of the nodes. Another popular method involves internally modeling a rigid connection element (i.e., a beam with one end pinned) that spans horizontally between each corner node to the next node in the finite element mesh. This enables the wall element to have moment continuity in the major direction (i.e., in the plane of the wall) by introducing a couple due to vertical shear. It is of some interest to note that shell elements are also used by some analyst to model shear walls. However, shell elements require some level of understanding of finite element principles and results from such elements should be interpreted and verified with some care. Some of the common behaviors that require scrutiny include numerical problems, such as “membrane locking” which happens for thin shells. Unlike beam, brace and column elements whose stiffness coefficients are integrated exactly, the plane stress finite element gives results that are “exact” or close to the theoretical solution, only if a finer mesh is used and convergence achieved. For most practical purposes, the use of only a single wall element in a typical bay may significantly underestimate deflections. In some cases, it could also give wrong results. Therefore, any finite element based analysis tool should have the option to generate a reasonably convergent mesh for wall systems in a building. It is due to the use and implementation of these fundamental principles and practices of finite element theory in modeling, particularly shear walls that the term “Finite Element-Based” analysis is used for describing analysis procedures discussed in this course. 4. Equations of Equilibrium and Motion In stiffness-based finite element methodology, the most important equation that governs the behavior and response of structures to static external loads is the static equilibrium equation. In matrix structural analysis, a static equilibrium equation for a structure subjected to gravity and lateral loads is expressed as: [K] {U} = - {F} (1) What most FE-based stiffness analysis programs do can be effectively summarized by Equation 1. The assembly of element and then global stiffness matrices together with the load vector, followed by the solution of the system equation and recovery of member forces, in a nutshell, constitute a static analysis. On the other hand, most building codes require a dynamic analysis for structures located in a seismically active area. There are essentially two ways of carrying out dynamic analysis for buildings subjected to earthquake loads, i.e., the equivalent static force procedure and a dynamic analysis procedure based on “accepted principles of dynamics”. Typical building analysis tools provide both analysis procedures for users. The equivalent static force procedure actually involves a static analysis that approximates the structures dynamic behavior. For buildings with stiffness, weight or geometric irregularity in plan or elevation, a true dynamic analysis procedure is required. A brief introduction of what constitute a dynamic analysis is given below. In dynamic analysis, the free vibration equations of equilibrium take the form: [K]{U} + M{ü} = {0} (2)The generalized eigenproblem can be formulated by assuming a periodic solution to the above problem and is of the form: [K] {F} = [M] {F} (3)Where [K] is the building lateral stiffness matrix and [M], the lumped diagonal mass matrix, and {U} the displacement vector. The process of eigenvalue extraction (also known as eigenproblem) consists of determining the frequencies ( w) and mode shapes (F) of the structure. The periods of the structure including the fundamental period are determined directly from the frequencies from their inverse relationships. The mode shapes, while useful alone as indicators of the behavior of the structure, are important in dynamic analyses such as modal superposition and response spectra. Figure 1. Building Frame with Wall, Beam, Column and Brace Elements.
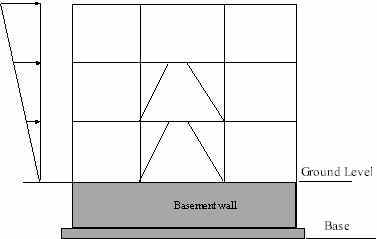
5. Analysis Criteria Items Most FE-based analysis tools assume default values for a number of general criteria items used in the analysis process. In most programs, these default values are set by the user during installation. One such criteria item is that of “rigid-end” or “panel” zones in beams and columns. The criteria item on “rigid end zones” lets users specify whether the deformation in these zones is to be considered or not. While deformation in these zones has been ignored by many engineers in the past, studies supported by observation of building behavior suggest that there is very significant amount of shear deformations in these zones. Assuming a reduction of 50% to account for these deformations is now an accepted practice in the industry even though it has no theoretical basis. Axial loads acting through lateral displacements of a structure cause additional displacements and forces. These effects commonly known as second-order effects, or alternatively as P-Delta effects, could produce significant loads and deformations that need to be considered in the design of building structures. The inclusion of these secondary effects in the analysis is specified through the “P-Delta” criteria item, used quite commonly in many analysis programs. Moment-frame and braced-frame buildings are typically sensitive to P-Delta effects and the consideration of these effects is required by almost all modern building codes for both static and dynamic analyses. Some programs allow specification of what is called “P-Delta scale factor”. This factor multiplies the effect of the weight of the floor that causes the P-Delta effects. The weight of a floor that participates in a secondary effect can be increased to account for live loads not included in the “mass dead load” by modifying the P-Delta “scale-factor”. The mass dead load is the total dead load weight that is supported by a floor diaphragm. The same scale factor can also be modified to account for factored load effects if LRFD code is used. It is instructional to note that the interaction of factored load effects in P-Delta needs to be considered as specified by the LRFD code [AISC, 1994]. For example, if 100% of the dead load is specified as the weight of the diaphragms and the applicable live loads are assumed to be 25% of that of dead load, the scale factor that includes factored load effects is given as below: P-Delta Scale Factor = 1.2 + 1.6(0.25) = 1.6. Another general criteria
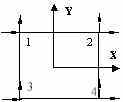
item that is used commonly is the “ground-level” criterion that helps users define the bottom
level of their lateral force resisting system. All program-generated loads
are applied to stories above the “ground level” as shown in
Figure 2. Both static and
dynamic analyses consider lateral displacement of stories above this level
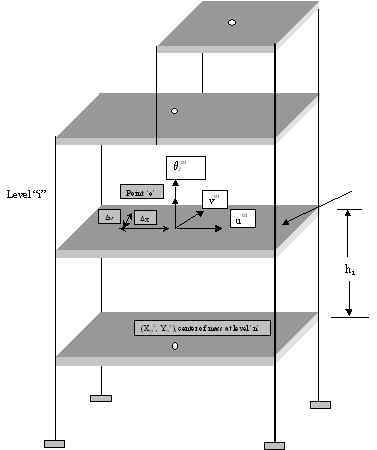
only. The in-plane stiffness of the floor systems of most building structures are extremely high compared to the stiffness of framing members. As a result, the in-plane deformations of beams can often be neglected, and columns, braces and walls connected to a given diaphragm will be constrained to move as one single unit in the lateral directions. This property is widely used in structural analysis to reduce the size of the system equations of buildings with such rigid floor types. When the “Rigid Diaphragm” option is selected for a given floor in any FE-based program, a transformation of coordinates and degrees of freedom is carried out to arrive at a system equation that allocates only three in-plane degrees of freedom for that particular diaphragm. The equations that govern the transformation of the in-plane lateral displacements of each member to that of the lateral displacements at the center of mass are:
where um, vm and qzm are the lateral displacements at the center of mass of a diaphragm, and Dy and Dx are the distances from the point of interest to the center of mass of the diaphragm. See Figure 4 for details.
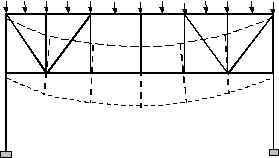
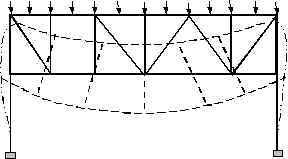
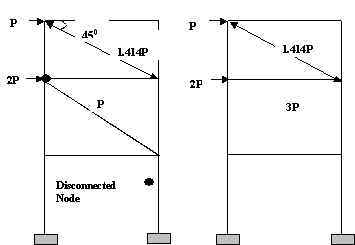
Figure 4. Typical Multistory Building with Rigid Floor Diaphragms. It is important to realize that there are many instances where the “rigid-diaphragm” assumption cannot be used. Buildings with multiple wings, light metal deck floors [usually used at roof levels], short shear-wall buildings are some of the examples where the floors cannot be assumed rigid diaphragms. Research has shown, for example, in the case of short shear-wall buildings such an assumption could give erroneous results because the walls have a comparable lateral stiffness to that of the floor diaphragms [Rutenberg, 1980, Boppana and Naiem, 1985]. On the other hand, the use of this important and realistic analysis assumption could give results that are sometimes not obvious. For example, the lateral and torsional displacement of unsymmetrical buildings subjected to gravity loads causes a significant redistribution of axial loads in columns and braces. The same assumption is also the reason why walls subjected to gravity loads might experience significant shear and bending moments. This is caused by differential vertical settlement which in turn forces the diaphragm to displace in the vertical and rotational direction resulting in redistribution of both vertical and horizontal loads. Another class of structures where the choice of this assumption has a significant bearing on the response of a numerical model of a structure is building or industrial structures with trusses. In the modeling of truss systems in a building or industrial structures, some engineers prefer disconnecting the interior nodes from the diaphragm in order to be able to evaluate the chord forces in the system. Experience has shown that the selection of nodes to be disconnected from a diaphragm has a strong bearing on the magnitude of chord forces evaluated. Disconnecting interior nodes and nodes at one or more supports allows the system to deflect more like a truss. On the other hand disconnecting only the interior nodes but leaving the supports connected to a diaphragm results in the truss system being rigidly suspended from the diaphragms. The axial forces in the top and bottom chords for these two systems could be drastically different. Figures 5.a and 5.b illustrate the behavior of such systems.
Figure 5.a. Truss with Only Interior Nodes Disconnected.
Figure 5.b. Truss with All Nodes Disconnected From Diaphragm. Another common example where the choice of nodes to be disconnected from a diaphragm has a bearing on the magnitude of member forces is the case of beams in braced frames. Figure 6.a shows a braced frame where both ends of a beam are disconnected from the diaphragm. The beam’s axial load, in this case, is just the horizontal component of the axial load of the brace spanning to it from the level above. Since both ends of the beam are disconnected from the diaphragm, any lateral load applied to the diaphragm at that level will not be transmitted to the beam. The additional load of 2P will be picked up by other members connected to the diaphragm, if there are any. If there are no members in the model, the program used may totally discard the load without even warning the user. However, if one of the ends of the beam is connected back to the diaphragm, this particular beam will pick additional axial loads as shown in Figure 6.b. It is important, therefore, to recognize that the design of these beams for collector forces depends strongly on the selection of these disconnected nodes.
a) both nodes of beam disconnected b) only one end of
beam disconnected Figure 6. Effect of Selection
of Disconnected Nodes on Axial Loads on Beams. While the proliferation of powerful structural analysis software has empowered engineers and architects to automate most of their analysis and design routines, the need for understanding the basic assumptions and theories used in these programs has also increased. It is only when users understand these basic principles and assumptions that they can arrive at a numerical model of their structure that very well approximates the real world external loads and the response of the structure itself. This course trains users of such programs with this in mind. 8. References and Further Readings 1. AISC, 1989, Manual of Steel Construction, Allowable Stress Design, 9th Edition, AISC, Chicago, IL, 1989. 2. AISC, 1994, Manual of Steel Construction, Load and Resistant Factor Design, 9th Edition, AISC, Chicago, IL, 1994. 3. ASCE, 1996, Minimum Design Loads for Buildings and Other Structures – ANSI/ASCE 7-95, American Society of Civil Engineers, 1996. 4. Bathe, K. J., “Finite Element Procedures in Engineering Analysis”, Prentice Hall, Inc., Englewood Cliffs, New Jersey, 1982. 5. Boppana, R. R. and Naiem, F., “Modeling Floor Diaphragms in Concrete Shear Wall Buildings”, Concrete International, Design and Construction, ACI, July 1985. 6. Naiem, Farzad, “The Seismic Design Handbook”, Van Nostrand Reinhold, NY, 1989. 7. Reddy, J. N., “Introduction to the Finite Element Method”, McGraw Hill, NY, 1987. 8. Wilson, E. L., Taylor, R. L., Doherty, W. P., and Ghaboussi, J., “Incompatible Displacement Models”, Numerical and Computer Models in Structural Mechanics, eds. S.J. Fenves, N. Perrone, A.R. Robinson, and W. C. Schnobrich, Academic Press, NY, pp. 43-57, 1973. 9. Kassegne, S.K., “FE-Based Three Dimensional Static and Dynamic Building Analysis”, March 1999, A Publication of RAM International, Carlsbad, CA 92008. |
Quiz
Once you finish studying the above course content, you need to take a quiz to obtain the PDH credits.
![]()
DISCLAIMER:
The materials contained in the online course are not intended as a representation
or warranty on the part of PDHonline.com or any other person/organization named
herein. The materials are for general information only. They are not a substitute
for competent professional advice. Application of this information to a specific
project should be reviewed by a registered professional engineer. Anyone making
use of the information set forth herein does so at their own risk and assumes
any and all resulting liability arising therefrom.
![]()