Calculate Factor of Safety Against Thread Stripping with A36 body

When a bolt is fully engaged into a nut or when a screw has a depth of engagement at least equal to the diameter of the screw, the thread engagement is adequae. Special situations arise when the bolt is not fully engaged into the nut or when the screw is engaged into a much weaker material. Sufficient design margin against failure by thread stripping should be provided.

Thread Engagement Issue

The determination of the required pre-load is outside the scope of this paper since it is dependent on the function of the joint, for eg. gasket seating, joint sealing, etc. A minimum residual pre-load stress of 20% of yield strength of the bolt is recommended by Ref. 8 for torque retention. Otherwise, torque retention devices such as lock nuts, jam nuts, lock washers, staking of threads, locking adhesives, etc would be required.

If this is an ASTM A193, Gr. B7 bolt, it would not have reached the plastic range since the von Mises stress is much less than the yield strength of the bolt (105 ksi).

See Reference 5.

Von Mises stress is given by combining tensile stress with shear stress as follows:

However, Code Interpretation III-1-91-15 states that Section NB-3232 does not apply to this situation. Thus, we could instead use Von Mises stress for combining tensile stress with shear and check against yield for ASME or non-ASME components

For an ASTM A93, Gr. B7 bolt, the allowable stress intensity would be 3 Sm, i.e. 3 x 35 ksi =105 ksi and has not been exceeded.

The shear stress is the highest at the periphery of the bolt cross-section which is also subject to an axial tensile stress. For ASME components, the rules of NB-3232.2 could be used to determine the maximum allowable stress. This requires calculating the stress intensity which is defined as twice the maximum shear stress or the difference between the principal stresses. Thus,

Note : The full applied torque is not experienced by the cross-section of the bolt since some of this torque goes to overcome friction under the nut head.

The shear stress is the thread torque divided by the polar section modulus.

Allowable Tensile Stess:

There is no clear guidance for the maximum allowable average tensile stress for preload. For ASME components, ASME III NB-3230 could be used. Provided differential thermal expansion does not create additional stresses, the maximum allowable average tensile stress could be considered as 2 x Sm since internal pressure would not increase the bolt loading. For ASTM A193 B7 at a service temperature of 200 deg. it would be 2 x 32.6 ksi and about 60% of yield.

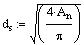
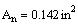
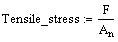
References:

1. Fastener Standards, 6th Edition, Industrial Fasteners Institute, 1988

2. AISC Manual of Steel Construction, 8th Edition, 1980

3. Mechanical Engineering Design, J.E. Slingley & L.D. Mitchell, McGraw-Hill

4. An Introduction to the Design and Behavior of Bolted Joints, by John H. Bickford

5. ASME Boiler & Pressure Vessel Code, Section III, 19?? Edition

6. Development of Design Charts for Bolts Preloaded up to the Plastic Range, N. Motosh, Journal of Engineering for Industry, ASME Aug. 76

7. Fastener Design Manual, Richard T. Barrett, NASA Reference Publication 1228, 1990

8. Bolted Joint Maintenance and Applications Guide, TR-104213, EPRI, December 1995

9. Specification for Structural Joints Using ASTM A325 or A490 Bolts, AISC, 1978

The author wishes to thank Dr. Yinyao Jiang, Dr. Peter Turula, and Bill Eccles for helping the author understand some technical points presented in this paper.

Acknowledgements:

i.e. Approx. 1/6 th turn

The required preload per Table 3 is 12000 lbs. Therefore, the rotation for 2400 lbs would be:

The bolt in this example has a preload of 2400 lbs. According to Table 4, the nut rotation for 1/2" A325 bolt would be 1/3 turn or 120 degrees for a bolt less than 4 diameters in length.

However, an approximate amount of nut rotation can be calculated based on Tables 3 and 4 of Reference 9.

Although it is theoretically possible to calculate the nut rotation as a function of the preload, it does not correlate well with observations for preloads less than yield. If tightening to preloads beyond yield strength is permissible, this is a cost effective and reliable method and is widely used for structural connections installing A325 or A490 bolts.

Calculation of Nut Rotation

Note: External threads used and methodology in Reference 1.

Method II

Using methodology in Reference 7.

for Carbon Steel; for Stainless Steel use 0.55

(Use the material property for the weaker material)

Method I:

2a is the angle of the thread and is 60 degrees for UNC thread

this is the distance between nut flats for hex nuts

dm is the effective contact diameter for the threads and is the average of major and minor diameters; It is also approximately equal to the pitch diameter.

TPI is threads per inch.

l is lead.

dc is the effective contact diameter between the nut and joint surface and is the average of major diameter and the distance between parallel nut flats for a hex nut.

Determine Torque vs. Tension Relationship

for 1/2" bolt with hex nut as the turning element

Set the parameter, i, according to the size of the bolt.

The following table gives bolt geometry and thread engagement data for UNC bolts from 1/4" diameter to 1 1/4" diameter. First row gives the major diamter, second row gives the minor diamter, third row gives the number of threads per inch, and the fourth row gives the distance between nut flats for hex nuts (1/4" to 5/8" sizes), and heavy hex nuts (3/4" to 1 1/4" sizes). The last two rows give the thread stripping areas per inch for external and internal threads respectively. This information is obtained from References 1 & 2.

Definitions:

S_m is the design stress intensity for the bolt material per ASME B & PV Code.
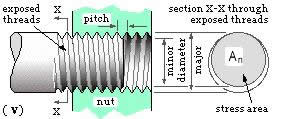
The major diameter is the largest diameter of a screw thread. It is also the nominal size of the bolt.
The minor diameter is the smallest diameter of a screw thread. Also referred to as root diameter.
The lead is the distance the nut moves parallel to the screw axis when the nut is given one turn. For a single start thread used in bolts, screws, nuts, etc., the lead is the same as the pitch and is the inverse of number of threads per inch.
The pitch diameter is the diameter of an imaginary coaxial cylinder cutting the threads at a height where the width of the thread and groove are equal. The average of major and minor diameters is approximately equal to the pitch diameter.
The stress area is the effective cross-sectional area of the bolt that resists bolt fracture.
The thread angle is the included angle between the flanks of a screw thread.

Introduction:

During maintenance activities in a power plant environment, the plant engineer is often called upon to make decisions concerning bolts in bolted connections in a variety of situations. Most of these bolts are torqued to achieve a pre-load rather than being tensioned with a tensioner. Examples include: increasing bolt torque beyond vendor manual recommended values to stop leaks, vendor recomendations for torquing are not available, bolt holes need to be enlarged to install replacement components, bolts may require trimming to accomodate replacement component, lack of thread engagement, etc. The ability to perform a component level analysis on a bolt, will provide the plant engineer an engineering tool to make the correct technical decision.

Progress Energy, Southport, NC 28461

by Clement Rajendra, PE

ds is the diameter based on stress area.

Tensile stress will be calculated using the stress area:

We can either use the results of the long or short formula for the value of F for this analyis.

Calculate maximum stress on the bolt during the torquing process:

This short formula gives results which compares well with the results of the long formula. However, it is important for the Nut factor to be selected carefully, since it significantly affects the results.

Nut factors are determined empirically. For values of Nut factor for various lubricated fasteners See Reference 4.

for unlubricated NEW steel fasteners

where

There is a simple empirical formula ("short formula") that is widely used in the industry to calculate the relationship between Torque and Tension. It is given by:

Suppose we apply a torque of 20 ft.lb.(240 in.lbs)

Further, it should be noted that only the torques represented by the first two terms will create a twist in the body of the bolt.

From this expression, it can be seen that bolt and thread geometry and the ceofficient

of friction significantly influence the relationship between torque and

preload. If the above expressions are evaluated it will be seen that only about 10% of the applied torque works to achieve the preload and the remainder works to overcome friction.

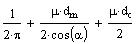
This expression can be mathematically simplified as such that

See Reference 3; "long formula"

Given an applied torque, T, the preload force F in the bolt is given by

T= F x Factor where:

m is the coefficient of friction assuming non-lubricated steel bolt and is assumed to the same for friction between threads and between nut and joint surface. A more realistic coefficient of friction for fasteners that has been in service may by 0.35-0.40 rather than 0.15.